Gambar Sketsa Grafik Fungsi Berikut: y = -(x-3)2 + 1

Ketemu lagi dengan kita sobat semua, kali ini kita akan membahas soal dan jawaban TVRI tanggal 5 Mei 2020 untuk siswa-siswi SMA/ SMK sederajat.

Ada 2 soal matematika yang harus sobat jawab pada materi Belajar dari Rumah TVRI kali ini, salah satunya berbunyi “Gambar sketsa grafik fungsi berikut: y = -(x-3)² + 1“.

Untuk menggambar sketsa grafik dari persamaan tersebut bagi sebagian siswa mungkin sangat susah, tapi jika sobat rajin berlatih mengerjakan soal semacam ini, lambat laun pasti bisa.

Langkah-langkah untuk membuat sebuah grafik kita harus terlebih dahulu mengetahui titik potong dengan sumbu x dan sumbu y, serta puncak kurvanya. Simak penjelasan di bawah ini.

Berikut soal dan jawaban TVRI 5 Mei 2020 SMA

Pertanyaan :

1. Diketahui fungsi y = x² – 4x + 3

Tentukan:

• a) Titik potong kurva fungsi dengan sumbu-sumbu koordinat.
• b) Koordinat titik balik minimum.

———————————————

2. Gambar sketsa grafik fungsi berikut: y = -(x-3)² + 1

———————————————

Jawaban :

1. a) Titik potong pada sumbu y saat x = 0
y = x² – 4x + 3
y = 0 – 0 + 3
y = 3

Titik potong pada sumbu x saat y = 0
y = x² – 4x + 3
x2 – 4x + 3 = 0
(x – 1)(x – 3) = 0
maka, x = 1 dan x = 3

Jadi titik potong HP {(0,3), (1,0), (3,0)}

b) Rumus titik balik minimum adalah x = -b^2a

y = x² – 4x + 3
a = 1, b = -4, c = 3

x = -(-4)²⁽¹⁾
x = 2

y = 2.2 – 4.2 + 3
y = -1

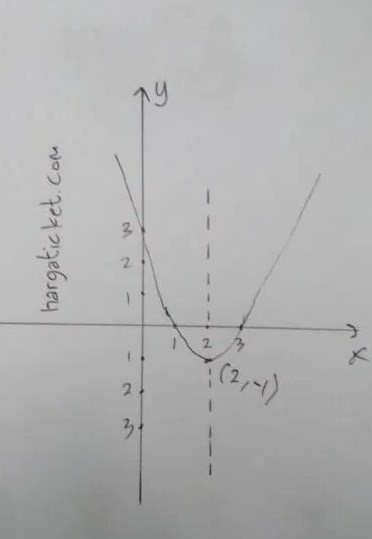
Jadi koordinat titik balik minimum adalah (2,-1), bisa dilihat pada gambar di bawah ini :

———————————————

2. Berikut sketsa grafik fungsi : y = -(x-3)² + 1

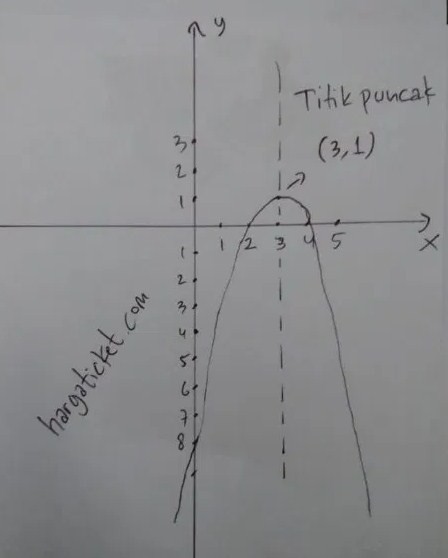
Penjelasan :

y = -(x-3)² + 1
y = – (x2 – 6x + 9) + 1
y = -x2 + 6x – 9 + 1
y = -x2 + 6x – 8

Sekarang kita mencari akar-akar dari persamaan di atas
y = -x² + 6x – 8 = 0
-x2 + 6x – 8 = 0 (dikali minus)
x2 – 6x + 8 = 0
(x – 4)(x – 2)
maka, x = 4 dan x = 2

Jadi titik potong dengan sumbu x adalah (4 , 0) dan (2 , 0)

Puncak grafik =
x = -b^2a = -6^2(-1)
x = 3

Masukkan nilai x pada persamaan soal di atas
y = -(x-3)² + 1
y = -(3-3)² + 1
y = -0 + 1
y = 1

Jadi titik puncak adalah (3,1)

Titik potong sumbu y saat x = 0, maka
y = -(x-3)² + 1
y = -(0-3)² + 1
y = -9 + 1
y = -8
Jadi titik potong sumbu y adalah (0,-8)

———————————————

Itulah jawaban dari soal “Gambar sketsa grafik fungsi berikut: y = -(x-3)² + 1″, semoga bermanfaat bagi semua.

source : hargaticket.com