Selamat siang sobat semua, kali ini kita akan membahas soal dan jawaban TVRI tanggal 5 Mei 2020 untuk siswa-siswi SMA/ SMK sederajat.
Ada 2 soal matematika yang harus sobat jawab pada materi Belajar dari Rumah TVRI kali ini, salah satunya berbunyi “Diketahui fungsi y = x2 – 4x + 3, tentukan Titik potong kurva fungsi dengan sumbu-sumbu koordinat dan Koordinat titik balik minimum“.
Karena materi belajar hari ini tentang Sketsa Grafik Fungsi Kuadrat, maka kita akan menjawabnya dilengkapi dengan sketsa grafik kurva.
Untuk menjawab soal ini sebenarnya cukup susah, apalagi bagi siswa-siswi yang tidak terlalu suka dengan Matematika. Oke, daripada makin bingung, simak jawabannya di bawah ini.
Berikut soal dan jawaban TVRI 5 Mei 2020 SMA
Pertanyaan :
1. Diketahui fungsi y = x2 – 4x + 3
Tentukan:
- a) Titik potong kurva fungsi dengan sumbu-sumbu koordinat.
- b) Koordinat titik balik minimum.
———————————————
2. Gambar sketsa grafik fungsi berikut: y = -(x-3)2 + 1
———————————————
Jawaban :
1. a) Titik potong pada sumbu y saat x = 0
y = x2 – 4x + 3
y = 0 – 0 + 3
y = 3
Titik potong pada sumbu x saat y = 0
y = x2 – 4x + 3
x2 – 4x + 3 = 0
(x – 1)(x – 3) = 0
maka, x = 1 dan x = 3
Jadi titik potong HP {(0,3), (1,0), (3,0)}
b) Rumus titik balik minimum adalah x = -b2a
y = x2 – 4x + 3
a = 1, b = -4, c = 3
x = -(-4)2(1)
x = 2
y = 2.2 – 4.2 + 3
y = -1
Jadi koordinat titik balik minimum adalah (2,-1), bisa dilihat pada gambar di bawah ini :
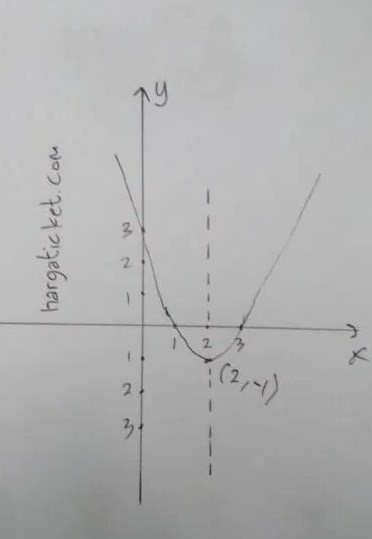
———————————————
2. Berikut sketsa grafik fungsi : y = -(x-3)2 + 1
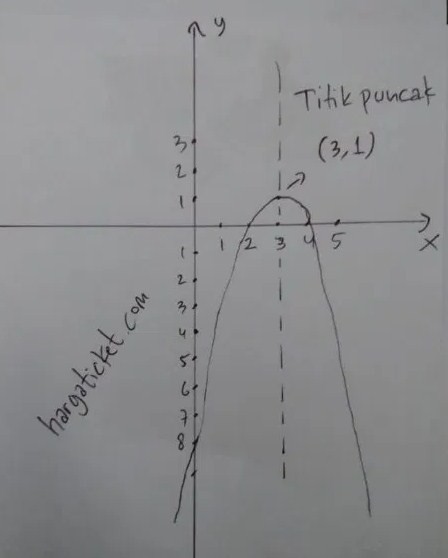
Penjelasan :
y = -(x-3)2 + 1
y = – (x2 – 6x + 9) + 1
y = -x2 + 6x – 9 + 1
y = -x2 + 6x – 8
Sekarang kita mencari akar-akar dari persamaan di atas
y = -x2 + 6x – 8 = 0
-x2 + 6x – 8 = 0 (dikali minus)
x2 – 6x + 8 = 0
(x – 4)(x – 2)
maka, x = 4 dan x = 2
Jadi titik potong dengan sumbu x adalah (4 , 0) dan (2 , 0)
Puncak grafik =
x = -b2a = -62(-1)
x = 3
Masukkan nilai x pada persamaan soal di atas
y = -(x-3)2 + 1
y = -(3-3)2 + 1
y = -0 + 1
y = 1
Jadi titik puncak adalah (3,1)
Titik potong sumbu y saat x = 0, maka
y = -(x-3)2 + 1
y = -(0-3)2 + 1
y = -9 + 1
y = -8
Jadi titik potong sumbu y adalah (0,-8)
———————————————
Itulah jawaban dari soal “Diketahui fungsi y = x2 – 4x + 3, tentukan Titik potong kurva fungsi dengan sumbu-sumbu koordinat dan koordinat titik balik minimum”, semoga bisa membantu sobat semua.
source : hargaticket.com